algorithms

递归扫盲贴

如果你对某块知识只有模糊的认识，那说明你还没有真正拥有它，用到的时候自然也会错误百出。这个时候仔细想想自己对哪些方面已经清楚了，哪些地方不明白，然后去找资料、看例子、写代码、思考总结，一步一步的剖析出它本质的过程，就能真正的拥有了它。

前面学习算法导论的时候遇到了一个不是很明白的问题，就是及其常见的递归和它的执行过程。最近看了些资料，也写了些代码，算是搞明白递归的执行过程了，记录如下，欢迎指正。

递归的定义和特点

首先得弄明白什么是递归，当然大家都知道它大概是个什么样子，怎么实现，但是具体的定义还是得翻一下课本。

在一个函数的定义中出现了对自己本身的调用，称之为直接递归；或者一个函数p的定义中包含了对函数q的调用，而q的实现过程又调用了p，即函数调用形成了一个环状调用链, 这种方式称之为间接递归。

用一个由 Python 实现的求阶乘函数的例子来说明这个定义及递归的一些基本特征。

1
2
3
4
5
6
7
8
9
10
11
12
13
'''
Created on Sep 20, 2013
@author: wenming.fu
'''
def fac(number):
    if number == 0:
        return 1
    else : 
        return number * fac(number-1)
#execute
if __name__ == "__main__":
    print fac(5)

从上面代码中可以清晰看到，fac()在定义函数体中调用了自己，符合直接递归的定义。

那么从这个简单的函数中看到了递归的哪些特征？

  • 正常的递归函数体最后总会有一个结束条件，称为递归出口，就是一个返回上一层递归的地方。上述例子中的 if number == 0 就是这么一个递归出口，当递归执行到这里的时候，会返回一个结果到上一层递归，这个时候意味着递归循环开始结束。

    如果递归的程序没有出口呢？一般会出现死循环，然后 Stack Overflow ，这种情况称为无穷递归(Infinite recursion)。但是在不同的编程语言中具体的表现各异。

    当我把上面这个程序的出口支路注释掉的时候，输出如下：RuntimeError: maximum recursion depth exceeded。为什么没有溢出呢？因为默认的 Python 有一个可用的递归深度的限制，以避免耗尽计算机中的内存。

    为什么像 Java 这样的编程语言中会出现溢出？贴一段资料说明下 Java 在调用一个方法的时候发生了什么。

    每当启用一个线程时，JVM就为他分配一个Java栈，栈是以帧为单位保存当前线程的运行状态。某个线程正在执行的方法称为当前方法，当前方法使用的栈帧称为当前帧，当前方法所属的类称为当前类，当前类的常量池称为当前常量池。当线程执行一个方法时，它会跟踪当前常量池。每当线程调用一个Java方法时，JVM就会在该线程对应的栈中压入一个帧，这个帧自然就成了当前帧。当执行这个方法时，它使用这个帧来存储参数、局部变量、中间运算结果等等。

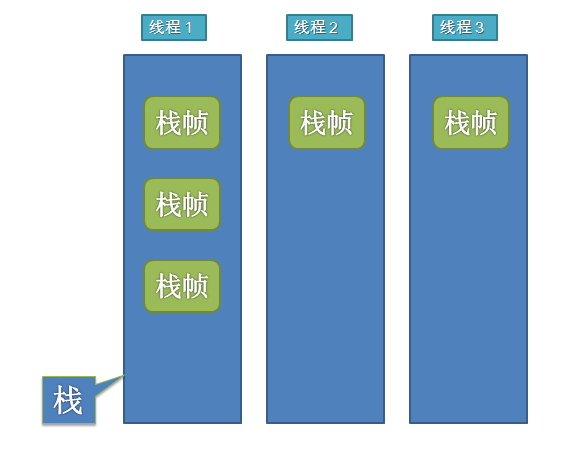
Java 栈帧示意图

黑体部分就是发生栈溢出的“罪魁祸首”，递归的过程中，没有停止循环的出口，在递归调用自身方法的时候不停的压栈，最终耗尽 JVM 分配的栈内存，就会发生溢出。这样看来当递归有出口的时候，如果需要保存的局部变量太多，递归层次太深等都可能导致溢出。

  • 有递归出口了还不够，还需要递归过程中修改函数的参数使递归出口能够到达。例子中，number 在递归中会持续的减去一，最终能符合 number == 0 这个条件，终止递归。

  • 不满足递归出口的情况，程序应该根据所求解问题的性质，将原问题分解成若干子问题，这些子问题的结构与原问题的结构相同，但规模较原问题小，这也是能够使用递归解决的问题的一个基本特征。这个问题的解能够根据子问题的解按照一定的规则组合得到，比如归并排序中，先把需要排序的序列从中间的元素分解成两部分，然后递归的分解左边的数列，递归的分解右边的数列，直到无法分解，执行 merge 把两个排好的序列合并成一个排好序的序列。具体过程可以参考我的文章 归并排序 。

递归的执行过程

递归的执行过程其实和它的执行原理有很大关系，下面用一个小例子说明。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
'''
Created on Sep 20, 2013
@author: wenming.fu
'''
def testRecursion(number):
    print number,id(number)
    if number == 1:
        print '............'
        print number,id(number)
        return
    testRecursion(number-1)
    for i in range(number):
        print number,
    print '',id(number)
        
if __name__ == "__main__":
    testRecursion(5)

其中，id(number)可以理解为返回number的内存地址，看到这段代码，你觉得运行的结果是什么样的？

下面是运行结果

1
2
3
4
5
6
7
8
9
10
11
5 10416744
4 10416756
3 10416768
2 10416780
1 10416792
............
1 10416792
2 2  10416780
3 3 3  10416768
4 4 4 4  10416756
5 5 5 5 5  10416744

是否和你所以为的一样，如果是一样的，那你可以不用看下面的一段了 :)

现在开始从这个运行结果解析递归的执行过程：

  1. 递归在执行到调用自己的时候就暂时中断当前的执行，直接进入下一层递归，当前的局部变量、执行结果等信息保存到栈里面。从运行结果中，递归调用自己前后，number 由 5、4、3、2、1 变成 1、2、3、4、5，证明了存储局部变量的数据结构是符合“先进后出”的栈。

  2. 每次调用重新生成局部变量、方法信息、运行结果等，然后压栈存储。可以看到在递归开始结束之前，number 的内存地址都不一样，但是在递归过程，每一层用到的局部变量是同一个，比如 number 值为 2 的时候，内存地址都是 10416780。

  3. 递归出口条件 if number == 1 被满足之后，程序将会执行到 return ，这个时候返回上一层递归 testRecursion(number-1) 处，并继续执行下面的代码，直到运行至函数隐式或者显式 return 语句，程序将会继续返回上一层递归处，直到栈空为止。

递归解决什么问题

由于递归会占用这存放局部变量等信息的空间，直到开始递归结束时才慢慢释放，而且程序在切换栈元素的时候消耗也比较大，我们如果不是在非常适合递归的场合，尽量不用递归来解决问题。

那么递归适合解决的问题是什么样子的？怎么写出能够解决问题的递归代码？简单说一下。

  • 递归算法适合解决问题规模不是特别大，问题能够被拆分成若干个子问题，且子问题的结构和原问题类似或者相同的问题。问题的解可以通过递归的结果拼接合并得到。

  • 适合递归算法解决的问题如果不用递归解决起来更复杂。这看起来矛盾，可是如果不用递归解决就已经很方便了，干嘛还用递归呢？如果用递归比不用还复杂，说明这个问题不适合递归。

递归解题用到的是分而治之(Divide and Conquer)的分治思想，先把问题分解成足够简单的子问题，通过解决子问题来解决整个问题。在开始确定递归算法之前，首先要对问题进行分析以确定下面的问题：1. 导致问题复杂的变量有哪些？ 2.问题和子问题相似点在哪儿？ 3.问题的边界值在哪儿，也就是递归出口在哪儿？ 4.确定解决这个问题的通式。

用二叉树的先序遍历递归实现来说明怎么解这类题目。先序遍历指的是在遍历这棵二叉树的时候首先访问根，再访问左（右）子树，最后访问右（左）子树的过程。二叉树如下：

二叉树

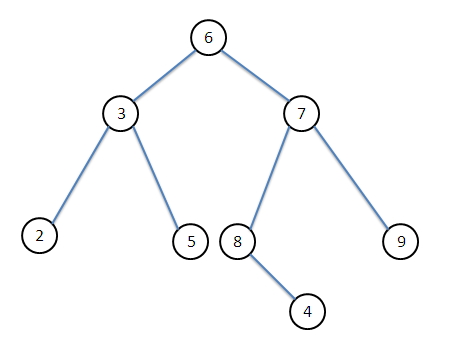
下面开始分析这棵树的先序遍历过程：

  1. 当二叉树只有一个根节点的时候，先序遍历的结果就是这个根节点。如二叉树只有 2 这么一个节点，那么遍历的结果就是 2 。

  2. 当二叉树只有一个深度为 1 的左（右）子树的时候，先序遍历的结果是先访问根节点，然后访问左（右）子树，如下图的二叉树访问结果是 3，2 。

1
2
3
  3
 /
2
  1. 当二叉树是一个深度为 1 的完全二叉树，那么先序遍历的结果是，先访问根节点（得到根节点的值），访问左子树，访问右子树。这个时候，可以将左（右）子树的情况看成 过程1 的情况，发现 过程1 其实就是这个问题的子问题，解决了 过程1 就等于解决了 过程3 。如下图的二叉树结果是3，2，1 
1
2
3
  3
 / \
2   1
  1. 由上面的分析得出了解决二叉树先序遍历的伪代码（通式）如下
1
2
3
4
DLR(tree):
    visit(tree.root)
    DLR(tree.LTree)
    DLR(tree.RTree)

总结一下：首先分析输入简单的情况，抓住问题的核心变量，找出问题的递归出口；慢慢增加变量的值，归纳出解决问题的通式；写出伪代码，并尝试调整为真正的代码。

Python实现

全文结束。